RS Aggarwal Class 12 Solutions Chapter 4
RS Aggarwal Solutions for Class 12 Chapter 4 – Inverse Trigonometric Functions Solutions PDF Download
RS Aggarwal Solutions Class 12 Maths Chapterwise – Free PDF Download
The RS Aggarwal Class 12 Solutions Chapter 4 are made to help you learn more about Inverse Trigonometric Functions. This chapter has 5 exercises and 126 questions. In this chapter, we’ll learn about what the inverse trigonometric functions are and how they work. The solutions to each exercise explain in detail how to find the main values of the given inverse functions. The RS Aggarwal Solutions for Class 12 Chapter 4 were made by experts in the field at Utopper.
RS Aggarwal Class 12 Solutions Chapter 4 teaches us how to graph the inverse trigonometric functions we’ve learned about in the previous chapter. It is a topic that comes up again and again in the most important All India Entrance Exams and the Class 12 Board Exam, so the RS Aggarwal class 12 Solutions Chapter 4 are a very important way to study for this chapter.
Click here to Buy Online RS Aggarwal Class 12 Book
RS Aggawal Class 12 Solutions Chapter 4 – Inverse Trigonometric Functions






























Download RS Aggarwal Class 12 Solutions Chapter 4 Inverse Trigonometry PDF
The RS Aggarwal Solutions for Class 12 Chapter 4 will be the best way for students to prepare for exams. The goal of the solution is to give the students the best and most trustworthy information about inverse trigonometry. Students will find it easier to learn if they look at the PDF solution, which will help them get better grades.
The RS Aggarwal Class 12 Solutions Chapter 4 will help you understand the idea of inverse trigonometry, its formulas, and how to solve the exercise sums. The PDF solution at Utopper is made by experts, so it is reliable and free of mistakes. The PDF of the answers is on our website, and you can get it for free.
RS Aggarwal Class 12 Solutions
Chapter-1 Relation Solutions
Chapter-2 Functions Solutions
Chapter-3 Binary Operations Solutions
Chapter-4 Inverse Trigonometric Functions Solutions
Chapter-5 Matrices Solutions
Chapter-6 Determinants Solutions
Chapter-7 Adjoint and Inverse of a Matrix Solutions
Chapter-8 System of Linear Equations Solutions
Chapter-9 Continuity and Differentiability Solutions
Chapter-10 Differentiation Solutions
Chapter-11 Applications of Derivatives Solutions
Chapter-12 Indefinite Integral Solutions
Chapter-13 Method of Integration Solutions
Chapter-14 Some Special Integrals Solutions
Chapter-15 Integration Using Partial Fractions Solutions
Chapter-16 Definite Integrals Solutions
Chapter-17 Area of Bounded Regions Solutions
Chapter-18 Differential Equations and Their Formation Solutions
Chapter-19 Differential Equations with Variable Separable Solutions
Chapter-20 Homogeneous Differential Equations Solutions
Chapter-21 Linear Differential Equations Solutions
Chapter-22 Vectors and Their Properties Solutions
Chapter-23 Scalar, or Dot, Product of Vectors Solutions
Chapter-24 Cross, or Vector, Product of Vectors Solutions
Chapter-25 Product of Three Vectors Solutions
Chapter-26 Fundamental Concepts of 3-Dimensional Geometry Solutions
Chapter-27 Straight Line in Space Solutions
Chapter-28 The Plane Solutions
Chapter-29 Probability Solutions
Chapter-30 Bayes’s Theorem and its Applications Solutions
Chapter-31 Probability Distribution Solutions
Chapter-32 Binomial Distribution Solutions
Chapter-33 Linear Programming Solutions

Let’s talk about Inverse Trigonometry some more:
RS Aggarwal Class 12 Solutions Chapter 4 Inverse Trigonometry
Inverse trigonometry is the opposite of the basic trigonometric functions, such as sine, cosine, tangent, cotangent, etc. You can also call these functions “arc functions” or “anti-trigonometric functions.” With the help of trigonometric ratios, these functions are used to find the angles. In the fields of engineering, geometry, and navigation, these functions are used a lot.
These functions are also known as “arc functions” because they calculate the arc length for any given trigonometric value. Inverse trigonometry is mostly used to do the opposite of what basic trigonometric functions do. The answers explain the basics of how inverse trigonometric functions work. It tells the reader how to use the formula in the chapter.
There are six formulas for inverse trigonometry. They are:
- Arcsine : sin-1(-x) = -sin-1(x), x ∈ [-1, 1]
- Arccosine : cos-1(-x) = π -cos-1(x), x ∈ [-1, 1]
- Arctangent : tan-1(-x) = -tan-1(x), x ∈ R
- Arccotangent : cot-1(-x) = π – cot-1(x), x ∈ R
- Arcsecant : sec-1(-x) = π -sec-1(x), |x| ≥ 1
- Arccosecant : cosec-1(-x) = -cosec-1(x), |x| ≥ 1
Detailed discussion of RS Aggarwal solutions for Class 12 Chapter 4 Inverse Trigonometric Functions
This course will teach you how to find the fundamental values of the inverse trigonometric functions given in the initial exercises.
- In the third and fourth exercises, you’ll need to prove some equations involving these functions.
- With the help of the basic properties, you will learn new properties and how to prove them in the exercises.
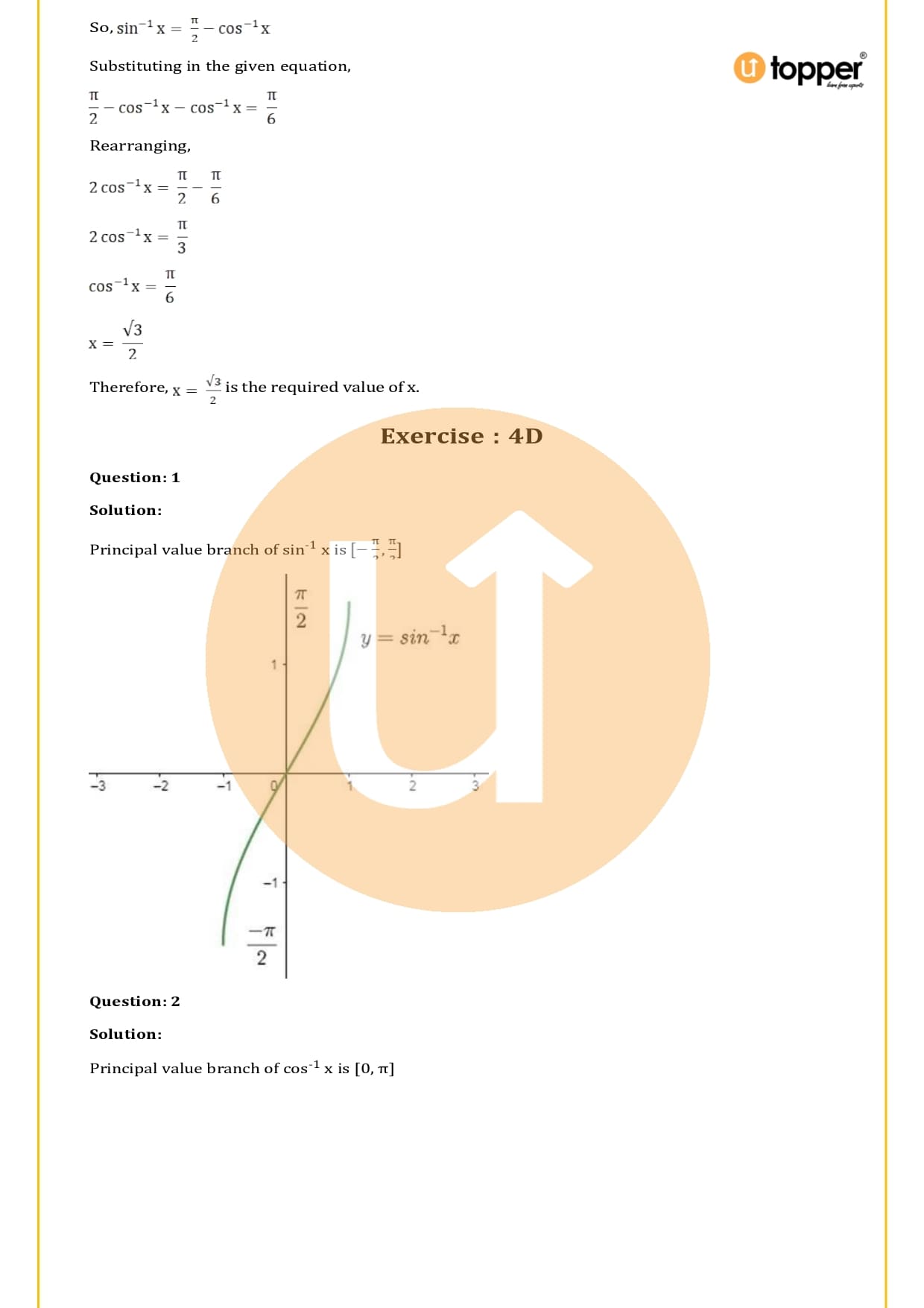
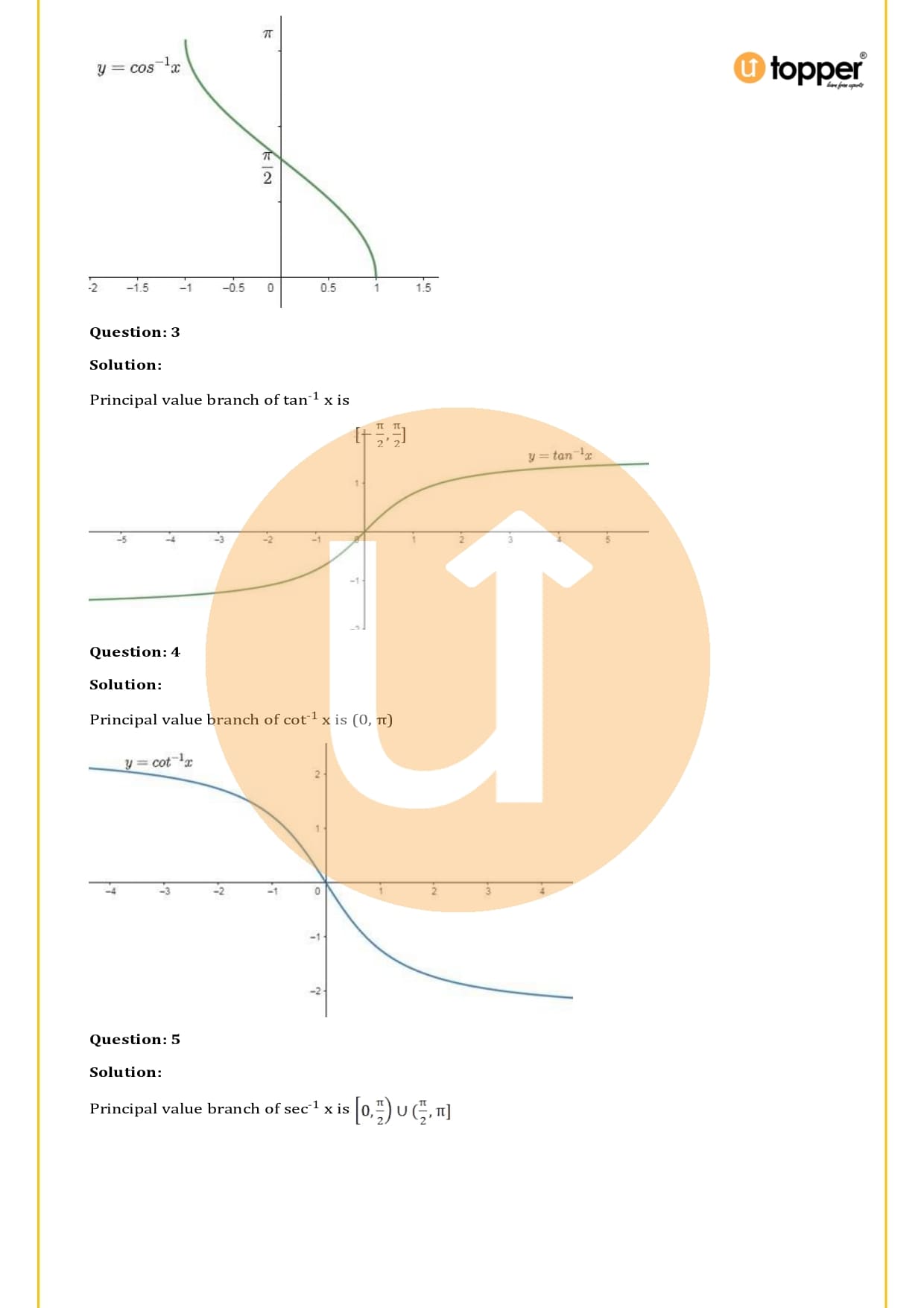
- In the fourth exercise, you will have to draw the graphs of different inverse trigonometric functions.
- The practise questions include both easy and hard ones for the RS Aggarwal Class 12 Solutions board exams and other important national-level entrance exams.
- The answers are written so that they cover all the important topics and are easy to understand.
FAQ ( Frequently Asked Questions )
1. What is an inverse trigonometric function, and how does it work?
Ans – Inverse trigonometry is the opposite of the basic trigonometric functions, such as sine, cosine, tangent, cotangent, etc. They are also called the arc functions, anti trigonometric functions, and cyclometric functions. When you do the opposite of trigonometric functions, you get the length of the arc that is needed to get the value you want.
With the help of trigonometric ratios, these functions are used to find the angles. In the fields of physics and navigation, these functions are used all the time. When you know the lengths of two sides of a right triangle, you can use the six important functions to find the lengths of the angles.
2. What are all six inverse trigonometric functions and formulas?
Ans – Arcsine, Arccosine, Arctangent, Arccotangent, Arcsecant, and Arccosecant are the six inverse trigonometric identities or functions. These functions are used a lot in engineering, physics, geometry, and other fields.
Here are the main formulas for inverse trigonometry:
- Arcsine : sin-1(-x) = -sin-1(x), x ∈ [-1, 1]
- Arccosine : cos-1(-x) = π -cos-1(x), x ∈ [-1, 1]
- Arctangent : tan-1(-x) = -tan-1(x), x ∈ R
- Arccotangent : cot-1(-x) = π – cot-1(x), x ∈ R
- Arcsecant : sec-1(-x) = π -sec-1(x), |x| ≥ 1
- Arccosecant : cosec-1(-x) = -cosec-1(x), |x| ≥ 1
3. From where I can download RS Aggrawal Class 12 solutions Chapter 4 ?
Ans – Students can get RS Aggarwal Class 12 Solutions Chapter 4 Trigonometric functions from the Utopper website or app. The experts who put together these solutions for Class 12 Mathematics know a lot about the subject and can help students prepare better for their exams.
4. How many exercises are in RS Aggrawal Class 12 Solutions Chapter 4?
Ans – This chapter is longer than the ones that came before it in RS Aggarwal Class 12 Solutions Chapter 4. In Chapter 4 of Class 12 Math, “Inverse of Trigonometric Functions,” there are a total of 126 questions spread across 5 exercises. These questions are meant to help students fully understand the chapter’s ideas and review what they’ve learned. In the first set of exercises, students learn about the values of inverse trigonometric functions. In later exercises, they learn about different proofs and properties of inverse trigonometric functions.
5. What are the Identities of Inverse Trigonometric Function ?
Ans – Inverse trigonometric functions have the following :
- sin-1 (sin x) = x provided –π/2 ≤ x ≤ π/2
- cos-1 (cos x) = x provided 0 ≤ x ≤ π
- tan-1 (tan x) = x provided –π/2 < x < π/2
- sin(sin-1 x) = x provided -1 ≤ x ≤ 1
- cos(cos-1 x) = x provided -1 ≤ x ≤ 1
- tan(tan-1 x) = x provided x ∈ R
- cosec(cosec-1 x) = x provided -1 ≤ x ≤ ∞ or -∞ < x ≤ 1
- sec(sec-1 x) = x provided 1 ≤ x ≤ ∞ or -∞ < x ≤ 1
- cot(cot-1 x) = x provided -∞ < x < ∞
- sin^(-1) = (2x)/(1 + x^2) = 2 tan^{-1}x
- cos^(-1) = (1 – x^2)/(1 + x^2) = 2 tan^{-1}x
- tan^(-1) = (2x)/(1 – x^2) = 2 tan^{-1}x
- 2cos-1 x = cos-1 (2×2 – 1)
- 2sin-1x = sin-1 2x√(1 – x2)
- 3sin-1x = sin-1(3x – 4×3)
- 3cos-1 x = cos-1 (4×3 – 3x)
- 3tan-1x = tan-1((3x – x3/1 – 3×2))
- sin-1x + sin-1y = sin-1{ x√(1 – y2) + y√(1 – x2)}
- sin-1x – sin-1y = sin-1{ x√(1 – y2) – y√(1 – x2)}
- cos-1 x + cos-1 y = cos-1 [xy – √{(1 – x2)(1 – y2)}]
- cos-1 x – cos-1 y = cos-1 [xy + √{(1 – x2)(1 – y2)}
- tan-1 x + tan-1 y = tan-1(x + y/1 – xy)
- tan-1 x – tan-1 y = tan-1(x – y/1 + xy)
- tan-1 x + tan-1 y +tan-1 z = tan-1 (x + y + z – xyz)/(1 – xy – yz – zx)

