RS Aggarwal Class 12 Solutions Chapter 10
RS Aggarwal Solutions for Class 12 Chapter 10 – Differentiation Solutions PDF Download
RS Aggarwal Solutions Class 12 Maths Chapterwise – Free PDF Download
The RS Aggarwal Class 12 Solutions Chapter 10 Differentiation are made so that students can learn how to solve the exercises. In this chapter’s RS Aggarwal Solutions, you’ll learn the basics of Differentiation for certain kinds of functions, which will help you move forward in Calculus. In the exercises, you mostly work with logarithmic, exponential, and inverse trigonometric functions. The big ideas in this chapter will also help you do well in your higher education. So, if you want a strong foundation, you need to do more than just read your school textbook.
The RS Aggarwal Class 12 Solutions Chapter 10 are on this page. They are made in a simple way to help students deal with the complicated terms and ideas they encounter when learning more advanced math. You should use the answers to study well for the test. These were made by experts to give full answers to the questions. Once you figure out these answers, you’ll be able to answer any hard question with ease.
Click here to Buy Online RS Aggarwal Class 12 Book
RS Aggawal Class 12 Solutions Chapter 10 – Differentiation


















































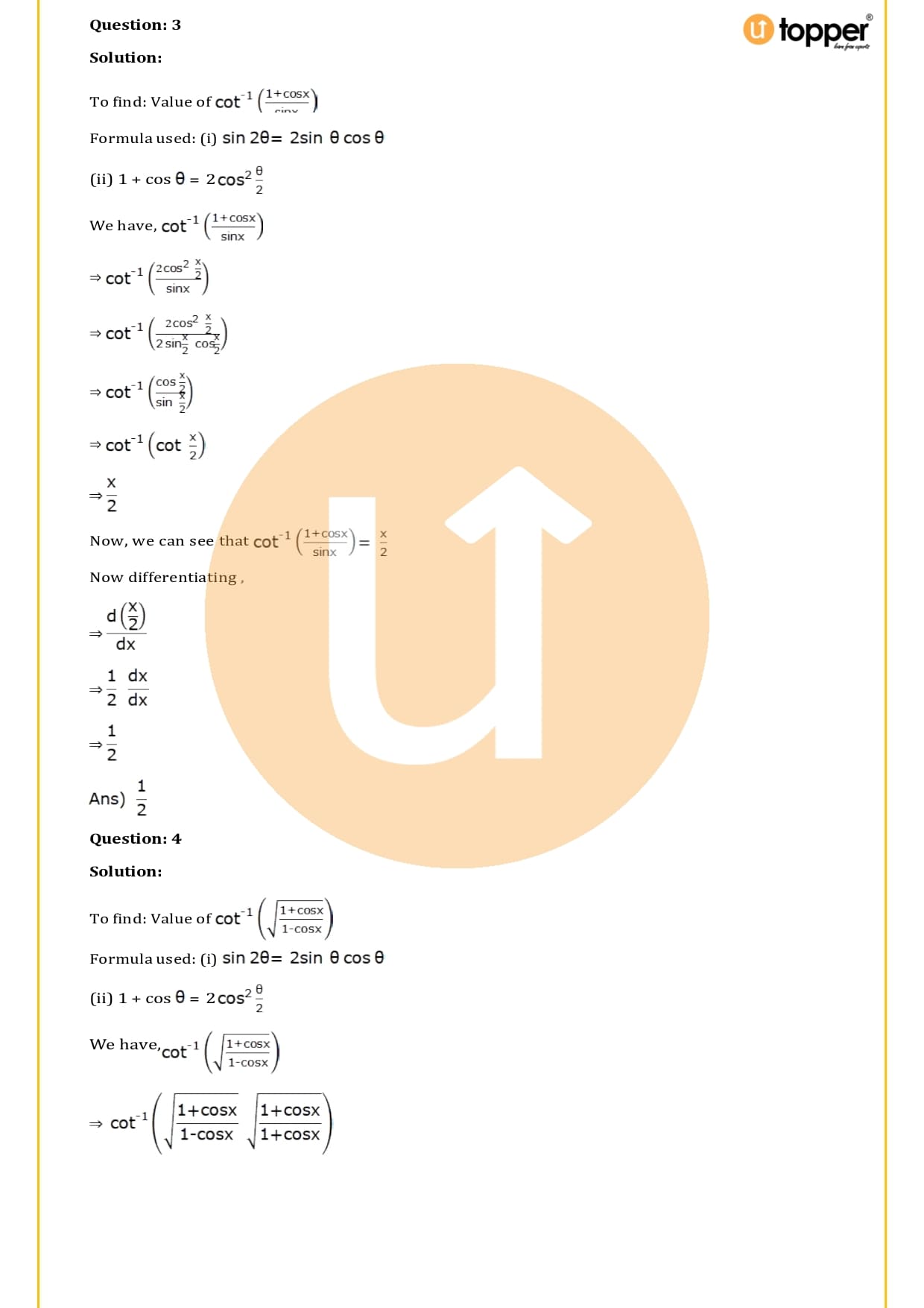
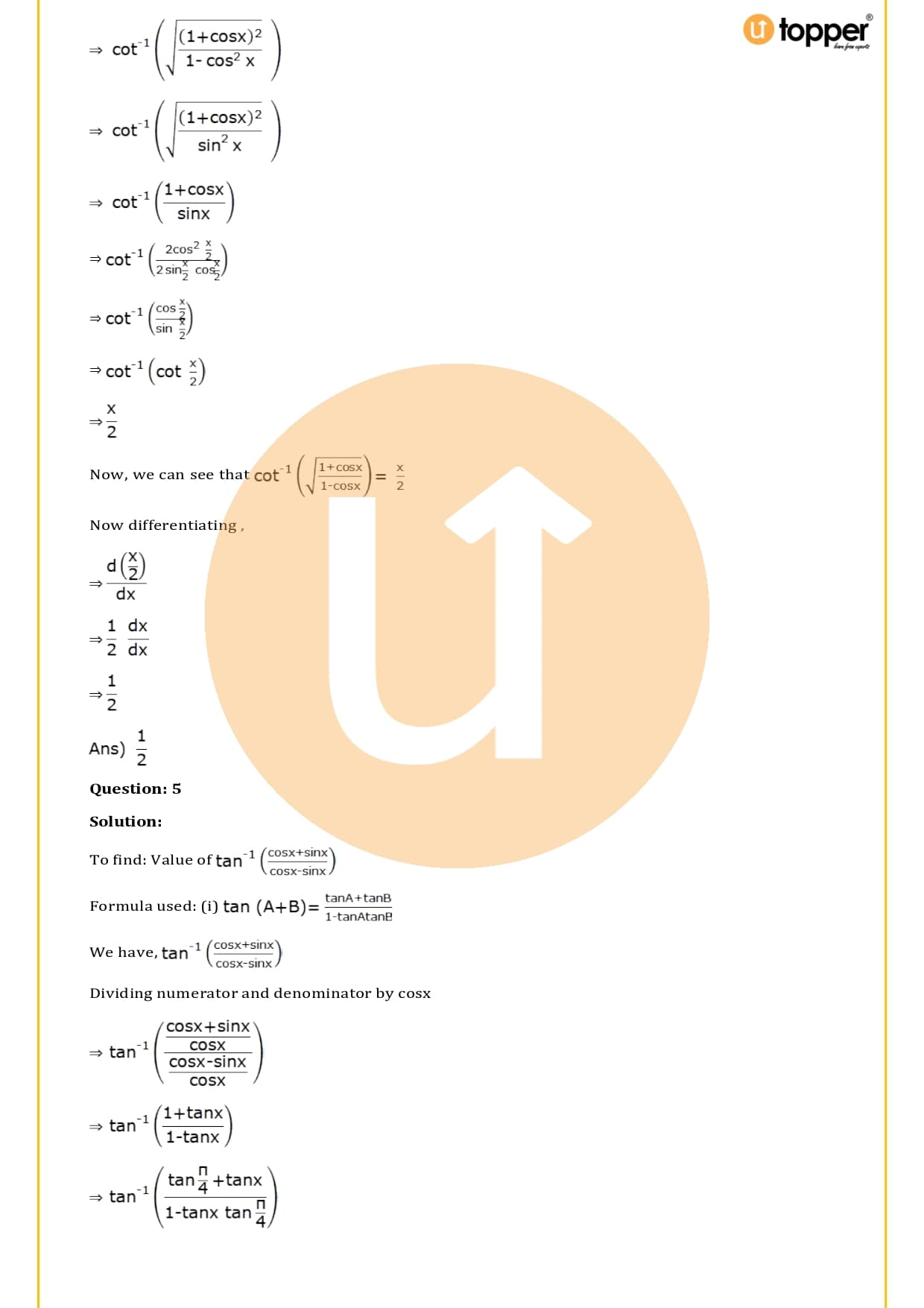



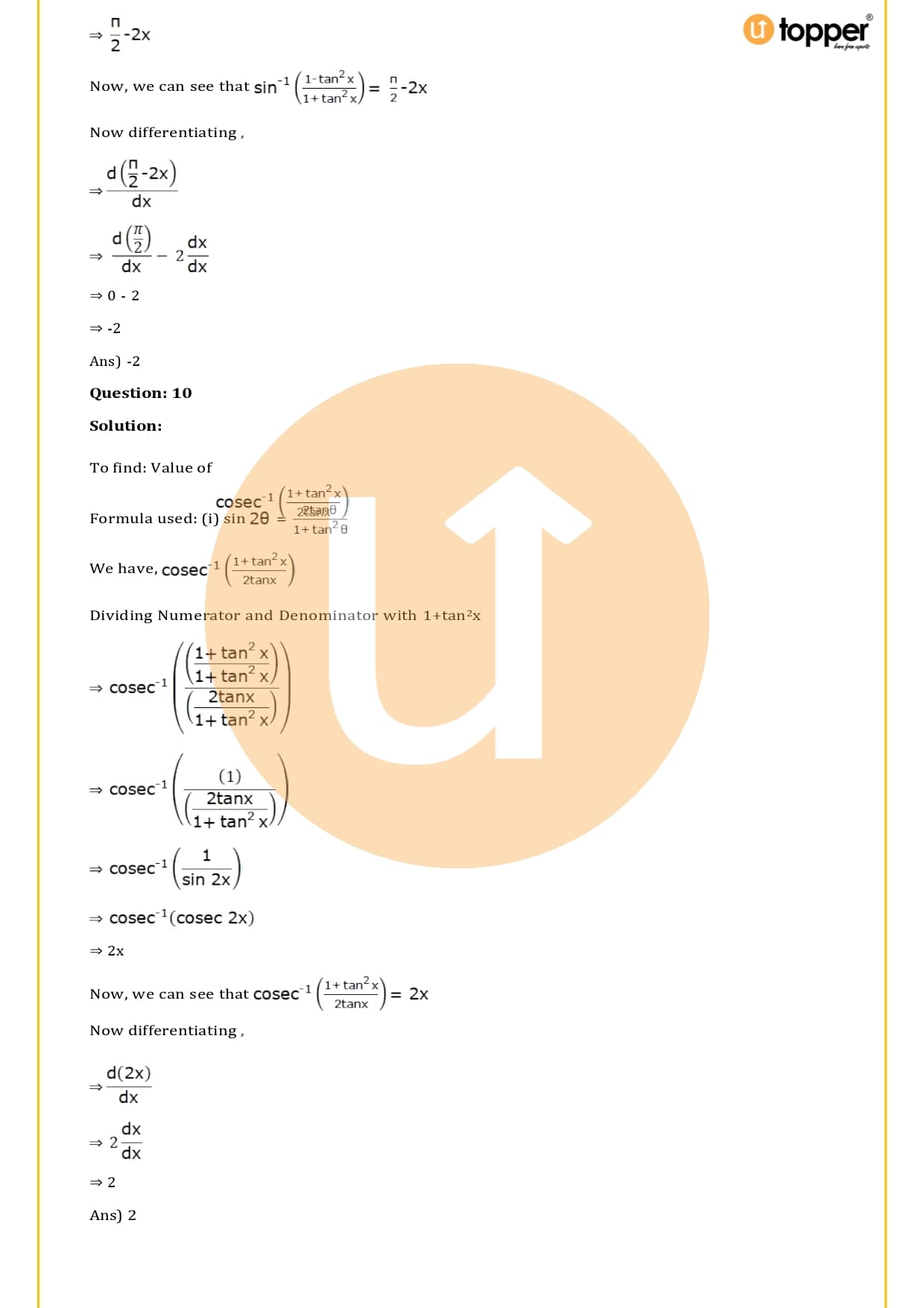


















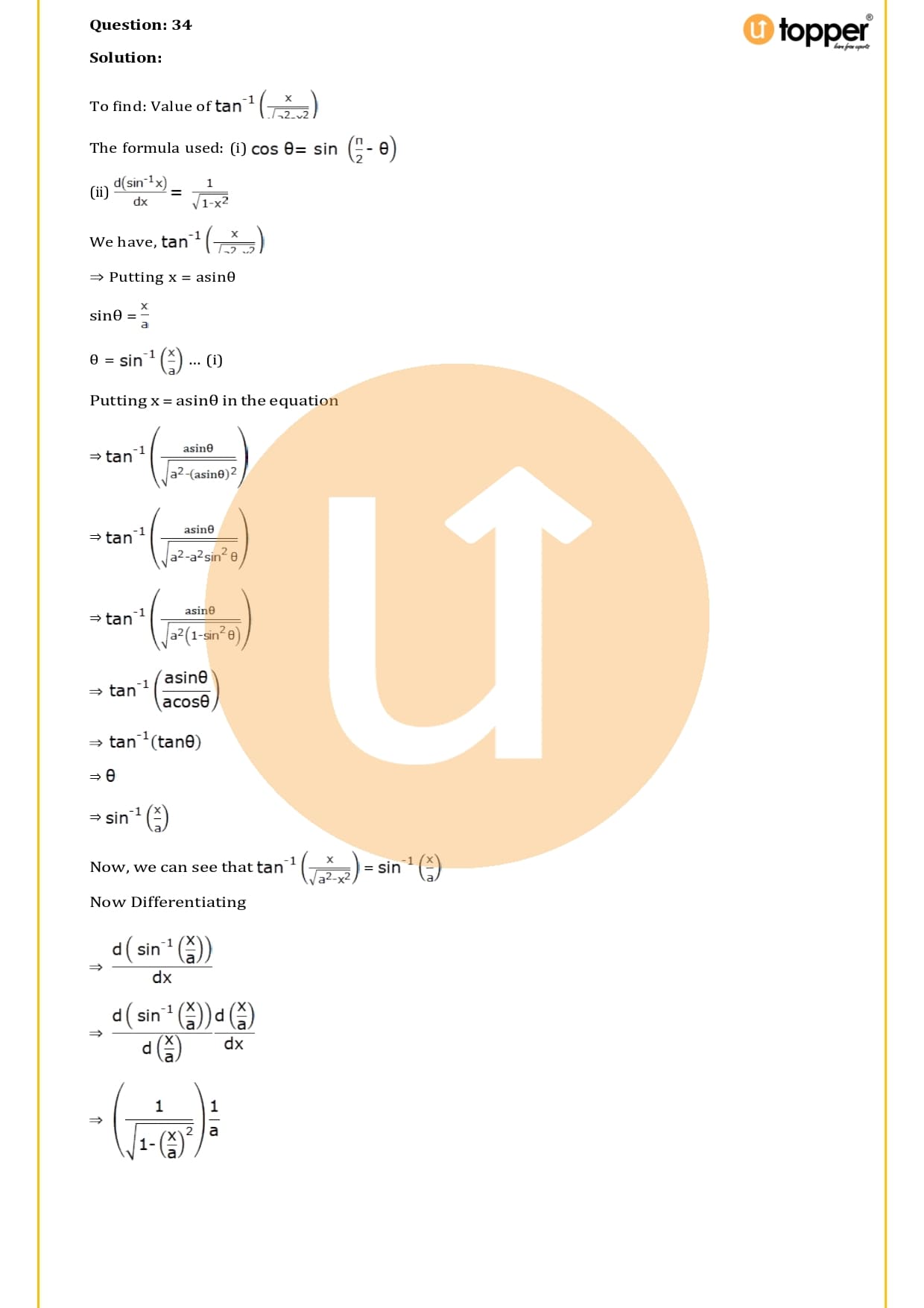



























































































Download the PDF of RS Aggarwal Class 12 Solutions Chapter 10 :
RS Aggarwal Class 12 Solutions Chapter 10 Differentiation can now be downloaded from the official Utopper website. The answers make it easy for students to look them up on the go. You can save these answers to any device you want. The offline download is very helpful, especially if you want to study for your test but don’t have access to the internet. You also like to keep these in hard copy.
This chapter has a total of 143 questions spread across 10 exercises. This will give you a lot of practise with differentiation, which is also a very important subject on competitive exams. These questions also go into detail about all the important functions in the CBSE curriculum. If you use this reference source as part of your study routine, you’ll be able to review quickly and understand the ideas completely. You can also use the answers to the exercises to do your homework. This will fill in any gaps that might have been left by what you learned in class.
RS Aggarwal Class 12 Solutions
Chapter-1 Relation Solutions
Chapter-2 Functions Solutions
Chapter-3 Binary Operations Solutions
Chapter-4 Inverse Trigonometric Functions Solutions
Chapter-5 Matrices Solutions
Chapter-6 Determinants Solutions
Chapter-7 Adjoint and Inverse of a Matrix Solutions
Chapter-8 System of Linear Equations Solutions
Chapter-9 Continuity and Differentiability Solutions
Chapter-10 Differentiation Solutions
Chapter-11 Applications of Derivatives Solutions
Chapter-12 Indefinite Integral Solutions
Chapter-13 Method of Integration Solutions
Chapter-14 Some Special Integrals Solutions
Chapter-15 Integration Using Partial Fractions Solutions
Chapter-16 Definite Integrals Solutions
Chapter-17 Area of Bounded Regions Solutions
Chapter-18 Differential Equations and Their Formation Solutions
Chapter-19 Differential Equations with Variable Separable Solutions
Chapter-20 Homogeneous Differential Equations Solutions
Chapter-21 Linear Differential Equations Solutions
Chapter-22 Vectors and Their Properties Solutions
Chapter-23 Scalar, or Dot, Product of Vectors Solutions
Chapter-24 Cross, or Vector, Product of Vectors Solutions
Chapter-25 Product of Three Vectors Solutions
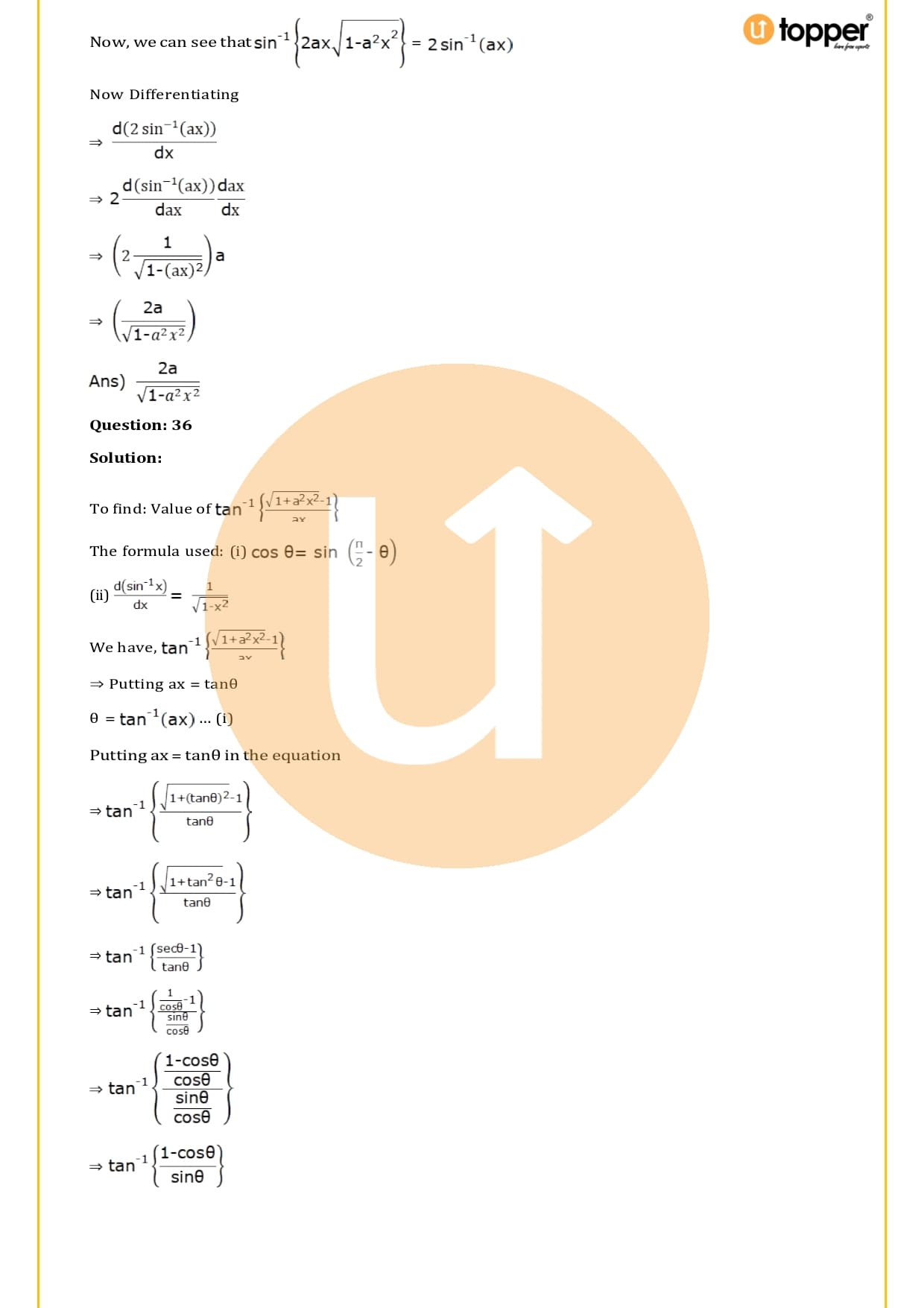
Chapter-26 Fundamental Concepts of 3-Dimensional Geometry Solutions
Chapter-27 Straight Line in Space Solutions
Chapter-28 The Plane Solutions
Chapter-29 Probability Solutions
Chapter-30 Bayes’s Theorem and its Applications Solutions
Chapter-31 Probability Distribution Solutions
Chapter-32 Binomial Distribution Solutions
Chapter-33 Linear Programming Solutions

There are four rules for differentiation.
These are the Sum and Difference Rules, the Product Rule, the Quotient Rule, and the Chain Rule.
1.Sum or Difference Rule
Derivatives are calculated as the sum or difference of two functions, i.e., a function is a sum or difference of two functions If f(x) = u(x) v(x), then f(x) = u(x) v(x) (x)
2. Product Rule
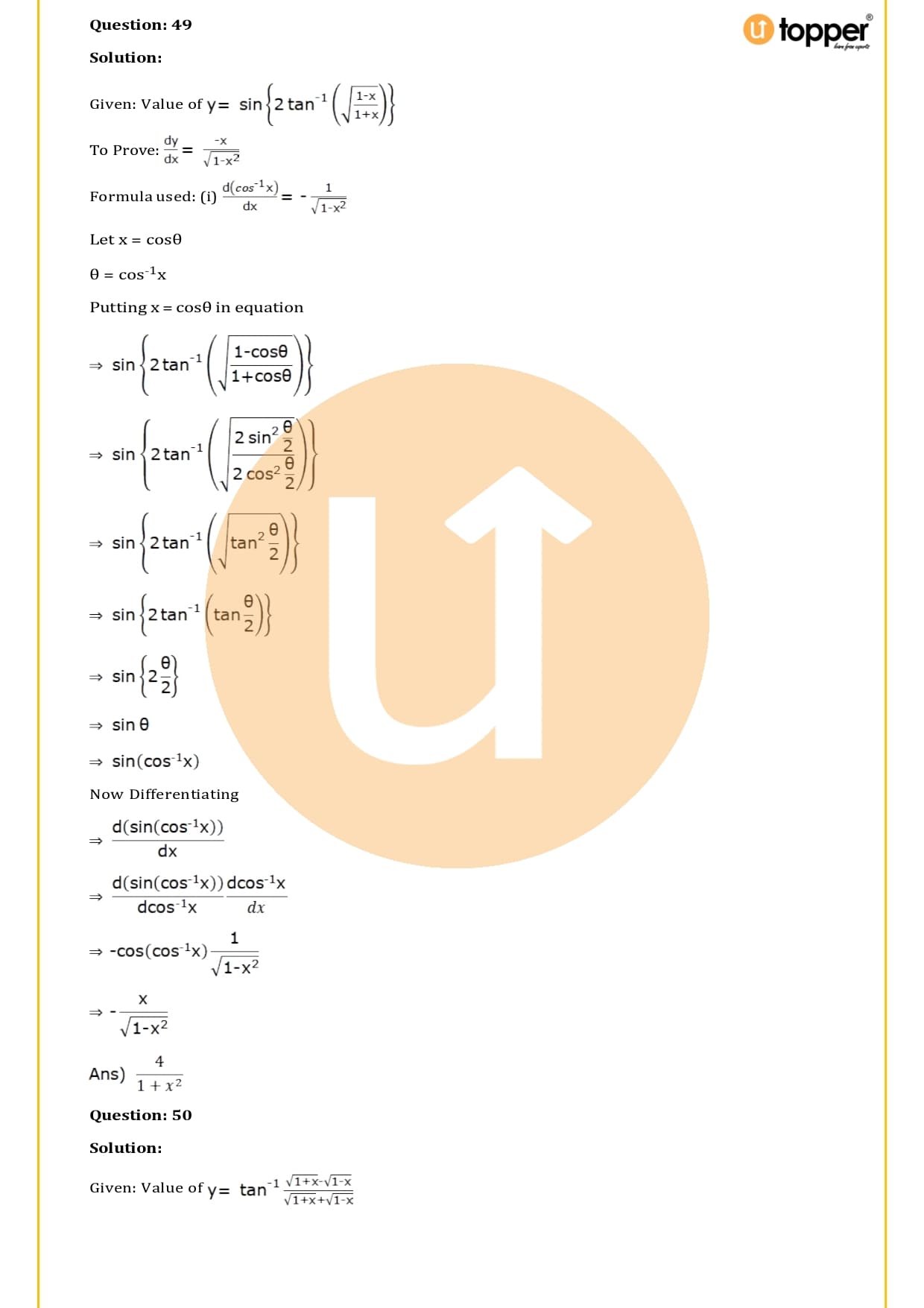
In the product rule, the function’s derivative is, when the function f(x) is the product of any two functions u(x) and v(x), If f(x)=u(x)×v(x) then, f′(x)=u′(x)×v(x)+u(x)×v′ (x)
3.Derivative of Inverse Function
If the function f(x) is made up of two functions, such as u(x)/v(x) and v(x), then the function’s derivative is If, f(x)=u(x)v(x) then, f′(x)=u′ (x) ×v(x)–u(x)×v′(x)
4. Chain Rule
If y = f(x) = g(u) for a function and u = h(x), then the chain rule for differentiation is: Dy/dx=dy/du×du/dx
Differentiation is a way to figure out how fast something is changing in relation to something else. Some of these are things like acceleration, which is the rate at which speed changes in relation to time. The derivative function is used to find the highest or lowest point in a curve in order to figure out where it turn With differentiation, you can find the curve’s normal and tangent.
Advantages of RS Aggarwal Solutions for Class 12 Maths Chapter 10 by Utopper
- The solutions are written as per the CBSE guidelines to assist you score well in your examinations.
- The answers from the experts at Utopper are written in very simple language to help you understand the topic.
- These answers are prepared by the experts of Utopper who have more years of teaching experience.
- By doing the exercises and reading other study materials like previous year paper class 12 , revision notes class 12 on Utopper, you can also learn how to manage your time well and become one of the best in your class.
- These solutions are written during a simple manner to maximize retention and improve understanding of the concepts.
- Solutions of every chapter are well categorized to enhance the convenience of use during your revisions.
FAQ ( Frequently Asked Questions )
1. What are the Inverse Trigonometric Functions Differentiation Formulas?
Ans – Trigonometric ratios are the same thing as inverse trigonometry functions. These inverse trigonometric functions are also called the arcus function, the cyclometric function, or the anti trigonometric functions. They are used to find the value of an angle for a given trigonometric value. Here are the formulas for the derivatives of functions that are the opposite of each other.
- d/dx (sin−1 x) = 1/ √(1–x2)
- d/dx (cos−1 x) = −1/ √(1–x2)
- d/dx (tan−1 x) = 1/(1+x2)
- d/dx (cot−1 x) = −1/(1+x2)
- d/dx (sec−1 x)= 1/ √(|x|x2–1)
- d/dx (cosec−1 x)= −1/ √(|x|x2–1)
2. What is a constant’s derivative value?
Ans – Trigonometric ratios are the same thing as inverse trigonometry functions. Here are the formulas from RS Aggarwal Class 12 Solutions Chapter 10 on Differentiation for the derivative of inverse trigonometric functions:
- d/dx (sin−1 x) = 1/ √(1–x2)
- d/dx (cos−1 x) = −1/ √(1–x2)
- d/dx (tan−1 x) = 1/(1+x2)
- d/dx (cot−1 x) = −1/d/dx (sec−1 x)= 1/ √(|x|x2–1)
- d/dx (cosec−1 x)= −1/ √(|x|x2–1)
- When a value stays the same, the derivative is 0. So, f(x) = 5 means that f'(x) = 0.
3. What kinds of topics do the exercises in RS Aggarwal Solutions for Class 12 Chapter 10 cover?
Ans – In RS Aggarwal Class 12 Solutions Chapter 10: Differentiation, there are a total of 10 exercises. These exercises help students go over everything they learned in the chapter and give them the practise they need. In the first four exercises of Chapter 10, most of the questions are about how to differentiate problems with inverse trigonometric, exponential, and logarithmic functions. The exercises that come next teach the students about differentiating the function of a function and other ideas like infinite series, parametric functions, and determinants.

