RS Aggarwal Class 11 Solutions Chapter 23

RS Aggarwal Solutions for Class 11 Chapter 23 – Ellipse PDF Download

RS Aggarwal Class 11 Solutions Chapter-wise – Free PDF Download

RS Aggarwal Class 11 Solutions Chapter 23 – Ellipse is a great way for students to study for Class 12 math because it helps them understand what they learned in Class 11. The methods and steps in RS Aggarwal for solving problems are written in a way that makes them easy for students to understand and helps them solve all kinds of problems. The Chapter of RS Aggarwal Solutions is easy to understand because the solutions and methods written by experts in the field are simple and easy to use.

There is one exercise in the chapter with 26 questions. These 26 RS Aggarwal Class 11 Solutions questions cover all of the important parts of the Chapter, so if you can answer them, you know the Chapter well. Now, the solved examples and answers to the questions save you time and make it easier for you to finish the course material. They also answer any questions you might have. With a small number of questions that cover all the concepts, you can practise again and again, and the best part is that you can access it 24 hours a day, 7 days a week.

We’ve made the whole course easy for you because our mentors not only teach you about the theory, but also give you plenty of real-world examples for each topic. Also Student can access free study materials like Revision Notes, Important Questions and many more. You won’t have to worry because the solutions are free and have no mistakes at all.

Click here to Buy Online The RS Aggarwal Class 11 Book Now

RS Aggarwal Class 11 Solutions Chapter 23 – Ellipse 

RS Aggarwal Class 11 Solutions Chapter 23

Why Class 11 Chapter 23 Ellipse Is Important?

Chapter 23 is short and very interesting. It’s called “ellipse.” Before taking on the problems in this chapter, students should make sure they understand the basics. The book RS Aggarwal has a great way of answering questions that are more focused on competitive exams. Every student who wants to use this PDF must first go over all of the basics and then start working on the RS Aggarwal problems.

To study this chapter, you need to know a lot about the ideas and topics on the course syllabus. As long as you understand the basics, you will be more confident in your ability to solve the problems in the different exercises.

RS Aggarwal Class 11 Solutions Chapter 23 – PDF

Students find it easy to get to the Utopper RS Aggarwal solutions for Class 11 Ellipse because they can download them easily at any time, on any device, and for free. This makes sure that they get the best resource for practise and that they understand the ideas in the chapter better.

Math is a very important subject, especially for people who want to go into engineering. It also has a lot of weight in competitive exams. Coordinate geometry is a great part of the Class 11 curriculum that teaches great ideas that will be useful in the years to come. Getting ready for and understanding these ideas takes a bit more practise. This is the main reason why students should keep the RS Aggarwal Solutions for Class 11 Ellipse close at hand and keep practising.

Ellipse is a plane that has two points that are the centre of attention. For every point on the curve, some of the distances between the two points stay the same.

Chapter 23 of RS Aggarwal Class 11 is about the following main ideas:
  • Major and minor axes of Ellipse.    
  • Horizontal and Vertical Ellipse.    
  • The ordinate and double ordinate of an ellipse.    
  • The special form of Ellipse.    
  • Position of any point concerning a given ellipse.    
  • Parametric equation.    
  • Equation of the chord of Ellipse.    
  • The eccentric angle of a given point.    
  • Concept of conformal points.    
  • Equation of normal and tangent of an ellipse
Tips for RS Aggarwal Class 11 Solutions Chapter 23

You can look at the syllabus to get a quick overview of all the main ideas and subtopics.

Start by putting together the necessary study materials for the chapter, such as the RS Aggarwal solutions for class 11 ellipse, so that you don’t get stuck while you’re getting ready.

First, look at the answers to figure out how to answer the questions, and then try it without them. This will help you get the most out of your study time and keep you from forgetting things. 

rs aggarwal class 11 solutions

FAQ ( Frequently Asked Questions )

1. What are the most important formulas in RS Aggarwal Class 11 Solutions Chapter 23?

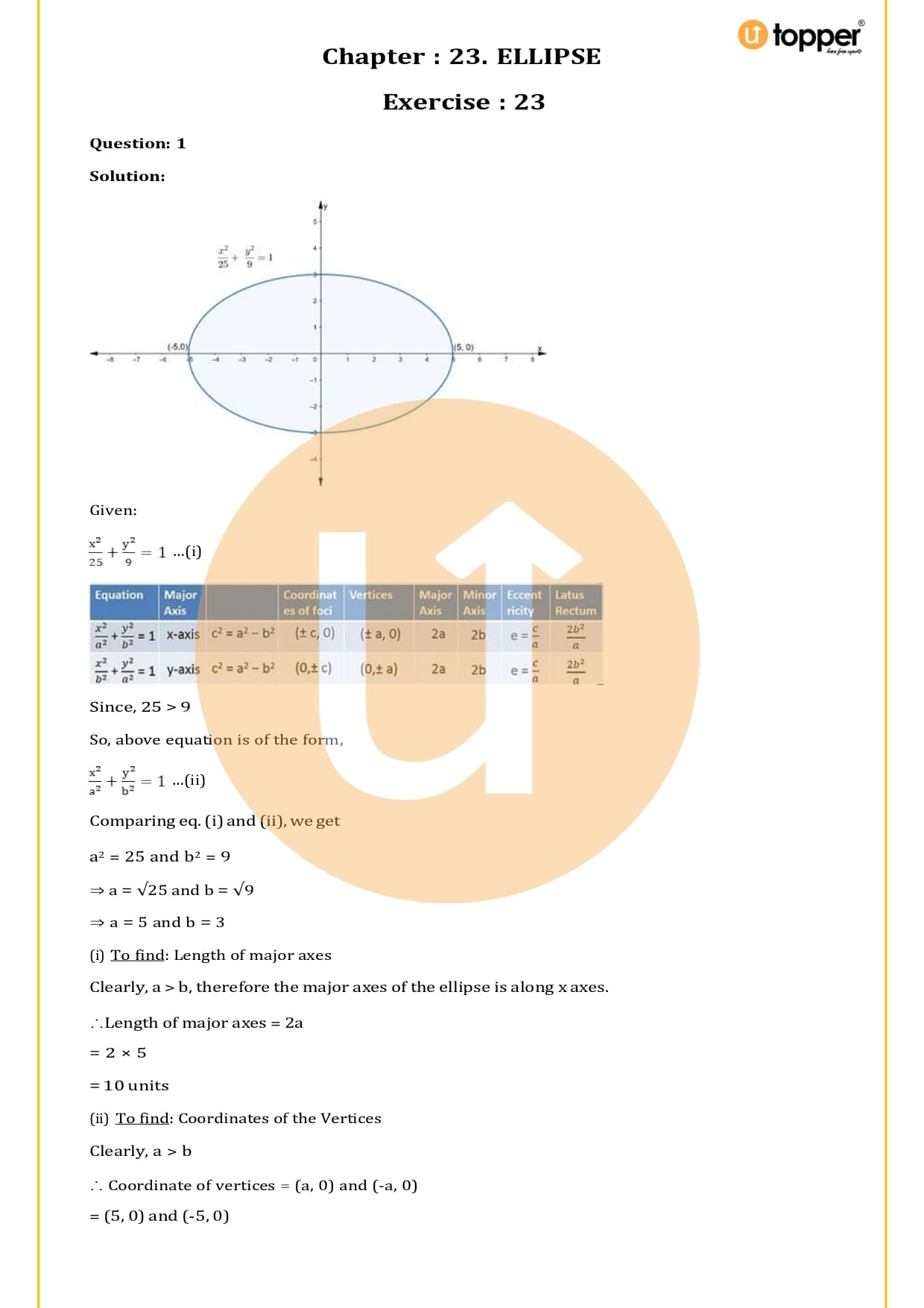
Ans – Important formulas for the general form of an ellipse, which is x²/a² + y²/b² = 1, are:

  • Major axis = 2a    
  • Minor axis = 2b    
  • Vertices = (±a, 0)    
  • Foci = (±c, 0)    
  • Eccentricity e = c/a    
  • Latus Recturm = 2b²/a

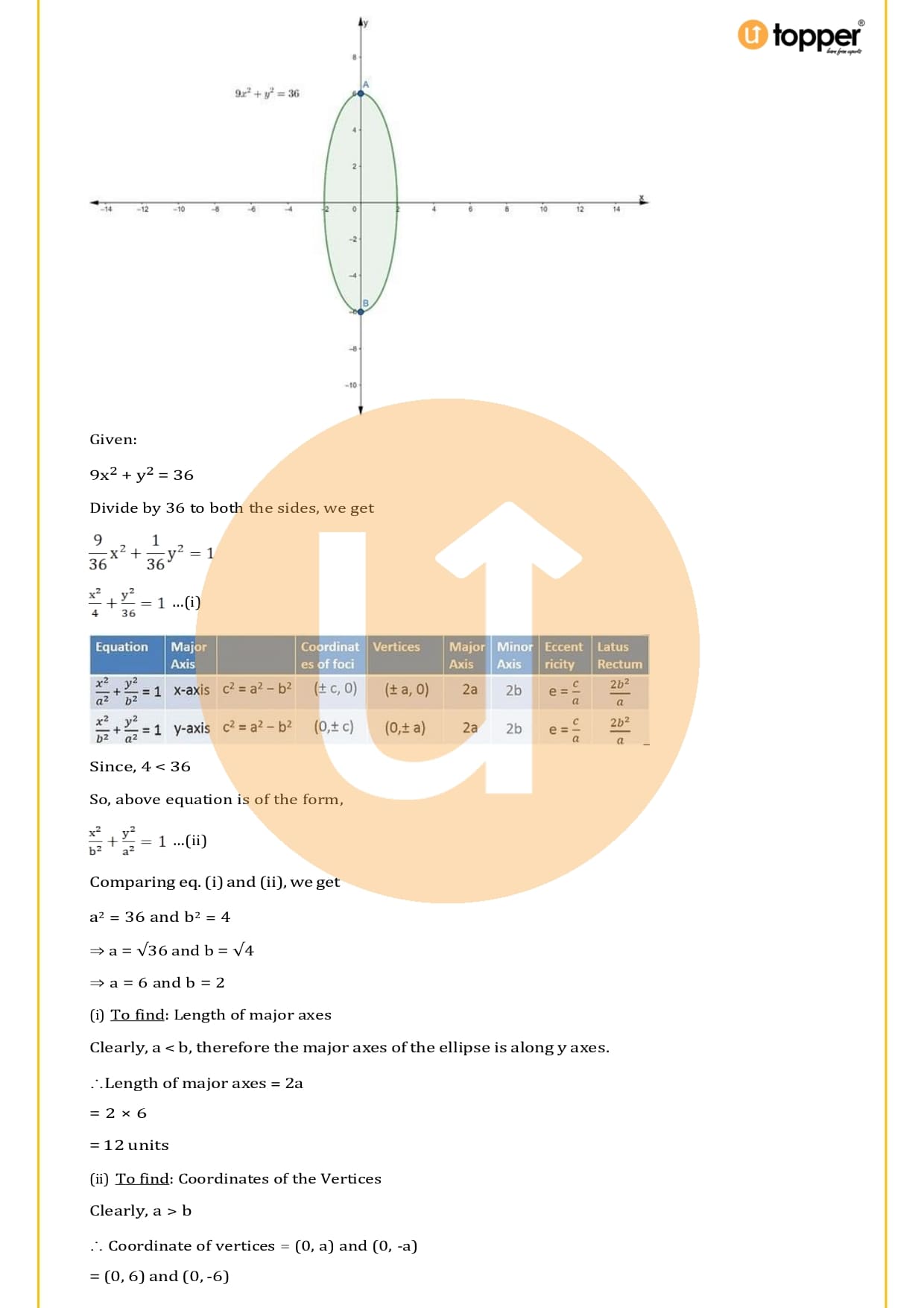
Important formulas for the general form of an ellipse, which is x²/b² + y²/a² = 1, are:

  • Major axis = 2a    
  • Minor axis = 2b    
  • Vertices = (0, ±a)    
  • Foci = (0, ±c)    
  • Eccentricity e = c/a    
  • Latus Rectum = 2b²/a

2. List five key ideas that can help you understand RS Aggarwal Solutions Class 11 Ellipse.

Ans – 5 ideas we learn about in this chapter are:

  • For a given point (x1, y1), the equation for the tangent to the general form of an ellipse, which is x2/a2 + y2/b2 = 1, is xx1/a2 + yy1/b2 = 1.
  • Any point on an ellipse can be used to draw four normals.
  • The axes of an ellipse and a given circle both have chords that are common to both.
  • If the centre of an ellipse is at (h,k) and the axes are parallel to the coordinate axes, then the equation of that ellipse is (x-h)2/a2 + (y-k)2/b2 = 1.
  • Two ellipse diameters are conjugate if each one cuts in half the chords that are parallel to the other.