Multiplication

In math, the product of two or more numbers is found by multiplying them together. It’s a basic math operation that comes up a lot in real life. We use multiplication to put together groups of the same size. Let’s find out more about how to multiply on this page.

Multiplication is an operation that can be thought of as adding the same number over and over again. The numbers that are multiplied together are called “factors,” and the result of multiplying two or more numbers together is called “the product of those numbers.” Multiplication is used to make adding the same number over and over again easier.

Multiplication as Repeated Addition

Example: In a Garden, 4 Roses are there on a branch. If there are 3benches in the garden, then how may Roses be there in all?

Solution– We can figure out the answer to this question by adding these numbers together, but it would take longer. So, 4 + 4 + 4 = 12 Roses. In other words, we can use multiplication when we need to work with bigger numbers.

Now, let’s solve this problem by multiplying. The number of roses in each branch will be multiplied by the number of branches. We can find out how many roses are there if we multiply 3 by 4.

Number of branches in the garden = 3

Number of roses on each branch = 4

Total Number of Roses = 3*4

Hence there are 12 roses in all.

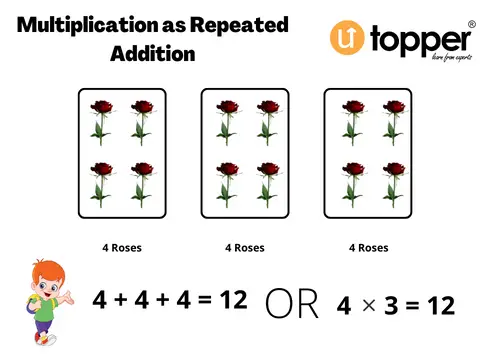
So, we can see that we end up with the same result in less time. This is why multiplication is also called “added over and over again.”

Multiplication Symbol (×)

There are different symbols in math. One of the math symbols that people use often is the symbol for “multiplication.” In the previous example, we learned how to multiply the numbers 6 and 9. When we look at the multiplication expression (6 9 = 54), we can see that the symbol () connects the two numbers and makes the expression complete. In addition to the cross symbol (), the midline dot operator () and the asterisk sign (*) can also be used to show multiplication.

Multiplication Formula

The multiplication formula is expressed as, Multiplicand × Multiplier = Product; where:

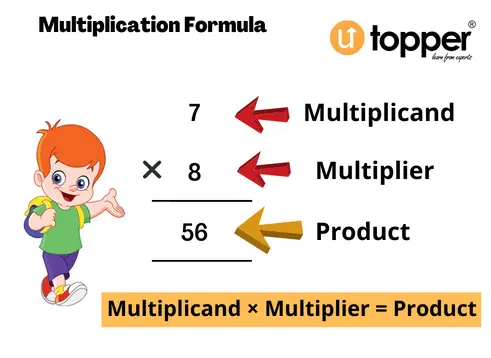
Multiplicand: The first number 

Multiplier: The second number 

Product: The final result after multiplying the multiplicand and multiplier.

Multiplication symbol: ‘×’ ( It is the symbol for multiplying (which connects the entire expression))

With the help of the following expression, let’s figure out how to multiply.

7(multiplicand) × 8 (multiplier) = 56 (product)

Let’s learn how to solve multiplication problems by using this simple idea of multiplication.

How to Solve Problems with Multiplication?

When solving multiplication problems, it is easy to multiply one-digit numbers by using multiplication tables. For larger numbers, however, we need to divide the numbers into columns based on their place values, such as ones, tens, hundreds, thousands, etc. There are two kinds of problems involving multiplication:

• Multiplication without regrouping
• Multiplication with regrouping

Let’s use examples to figure out what’s going on in each case.

Multiplication Without Regrouping

When you multiply two numbers without regrouping, you use smaller numbers that don’t need to be moved up to the next place value. It is the basic level that could help a learner understand the basics of multiplication before moving on to the higher-level problems that include regrouping. Let’s see how this works with the help of an example.

Example: Multiply 2304 by 2.

Solution:

Step 1: Start with the digit in one’s place. (2 × 4 = 8)

Step 2: Multiply 2 with the digit in the tens place. (2 × 0 = 0)

Step 3: Now, multiply 2 with the digit in the hundreds place. (2 × 3 = 6)

Step 4: Now multiply 2 with the digit in the thousands place. (2 × 2 = 4)

Step 5: 2304 × 2 = 4608.

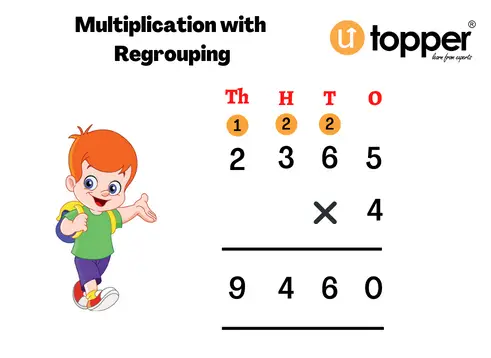
Multiplication With Regrouping

When you regroup and multiply more than two numbers, the result is a number with two digits. In this kind of multiplication, we need to take a carry-over to the next higher place value. Let’s see how this works with the help of an example.

Example: Multiply 2365 with 4

Solution: Let us multiply 2365 × 4 using the steps given below and try to relate them with the figure given after the steps.

Step 1: Start with the digit in one place, that is, 5 × 4 = 20 ones which means 2 tens 0 ones. Now, carry 2 tens to the tens column.

Step 2: Multiply 4 with the digit in the tens place, that is, 4 × 6 = 24 tens. Now, we will add this to the carry-over. This means, 24 + 2 (carry-over from step 1) = 26. Carry 2 to the hundreds column.

Step 3: Multiply 4 with the digit in the hundreds place, that is, 4 × 3 = 12 hundred. Now, let us add this to the carry-over from the previous step. This means, 12 + 2 (carry-over from step 2) = 14. We will again carry 1 to thousands of columns.

Step 4: Multiply 4 with the digit in the thousands place, that is, 4 × 2 = 8 thousand. So, let us again add this to the carry-over, that is, 8 + 1 (carry-over from step 3) = 9

Step 5: Therefore, the product of 2365 × 4 = 9460.

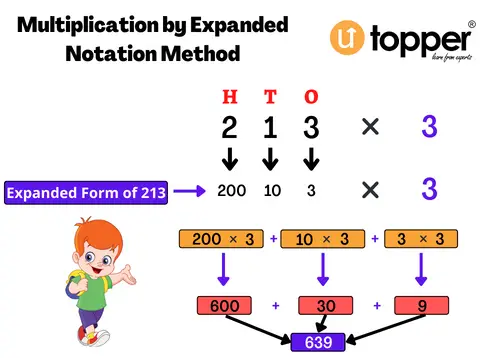
Multiplication Using Expanded Notation Method 

This method is also called the Row Method 

Example: Multiply 213 by 3 

Solution – 

213 * 3 = ( 200 + 10 + 3 ) * 3

( 200 * 3 ) + ( 10 * 3 ) + ( 3 * 3 ) 

600 + 30 + 9 

639 

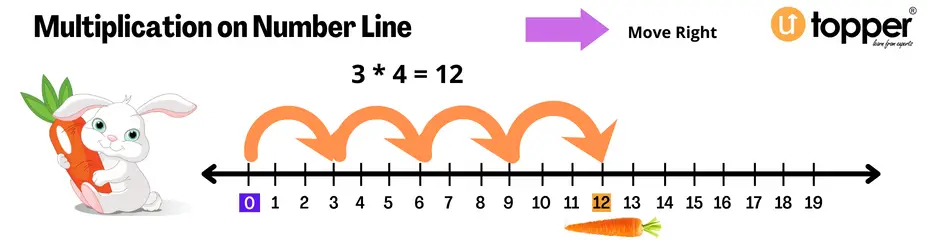
Multiplication Using Number Line

Multiplication on a number line is the process of using a number line to multiply a given set of numbers. A number line is a straight line that shows the numbers from 1 to 10. We know that multiplication is the same as adding over and over again. So, to do multiplication on a number line, we start at 0 and move the given number of times toward the right side of the line.

Example: Use a number line to find the answer to 3 x 5.

Solution: Look at the number line below to see how 3 × 4 = 12 works. We’ll start at 0 and move right along the number line. We will divide into 3 groups of 4 people each. This brings us to the number 12.

The line above shows that 3 times 4 is 12. This can also be written as 3 + 3 + 3 + 3 = 12. The statement about multiplication is written as 3 × 4 = 15.

Property of Multiplication 

1. Order Property – Commutative Property

The product of two numbers does not change when we change the order of the numbers 

Example : 25 × 13 = 13 × 25 = 325 

2. Grouping of Numbers – Associative Property

The Product of three numbers does not change when we change the Grouping of the numbers

Example : 24 × ( 38 × 16 ) = ( 24 × 38 ) × 16 = 14592

3. Multiplicative property of 1 – Identity Property

The product of a number by 1 is the number itself 

Example : 143 × 1 = 143 

4. Multiplicative property of 0 – Zero Property

The product of a number by zero is always zero

Example : 563 × 0 = 0 

Multiplication Word Problems

Multiplication word problems are easy to solve if you look at the situation carefully and find the answer. Let’s use a fun example to learn about the theory behind real-life multiplication word problems.

Example: A Bouquet has 235 flowers. How many flowers are there in 4 such bouquets? 

Solution – 

Number of flowers in a bouquet = 235 

Number of bouquet = 4

Step 1: Start with the digit in ones place. Multiply 4 × 5 = 20. Now carry 2 to the tens column.

Step 2: Multiply 4 with the digit in the tens place, that is, 4 × 3 = 12. Now, add this to the carry-over from the previous step. 12 + 2 (carry-over from step 1) = 14. From this, carry 1 to the hundreds column.

Step 3: Multiply 4 with the digit in the hundreds place, 4 × 2 = 8 hundred. 8 + 1 (carry-over from step 2) = 9.

Step 4: Therefore, the product of 235 × 4 = 940.

Total number of flowers in 7 bouquets = 235 × 4 = 940 

Multiplication tips and tricks:

Here are some tips and tricks that can be used when multiplying numbers.

• When you multiply, it doesn’t matter what order the numbers are in. So choose the order that makes you feel most at ease. Students may find it easier to remember 4 9 on the multiplication table than 9 4.
• When you multiply three numbers, pick the two that are easiest to multiply. For example, it will be hard to multiply 5 17 2 if we first try to multiply 5 17. Instead, adding 5 and 2 together gives 10, which is easy to multiply by 17 to get 170.
• When multiplying a two-digit number by a one-digit number, it can help to break the two-digit number into its place values. Then multiply each part by itself and add. For example, 374 can be mentally solved by dividing 37 into 30+7. So, 30 times 4 is 120, and 7 times 4 is 28. So, the answer is 148, which is 120 plus 28. When written down, this may seem like more work, but it’s much easier to figure out in your head.
• Even if you can’t remember the multiplication fact, it’s easy to figure out in your head. For example, it’s hard to remember 17 9. But this can be rearranged in your mind as 17 (10 – 1). So, 170 minus 17 is equal to 153.

Multiplication Examples : 

Example 1: One Comic Book has 764  pages. How many pages are there in 7 such comic books? 

Solution : 

Number of pages in 1 Comic Book = 764 

Number of pages in 7 Comicbooks = 764 × 7 = 5348 

Example 2: Solve the following multiplication word problem. Find the Product of 327 by 26. 

Solution – 

FAQ ( Frequently Asked Question ) of Multiplication