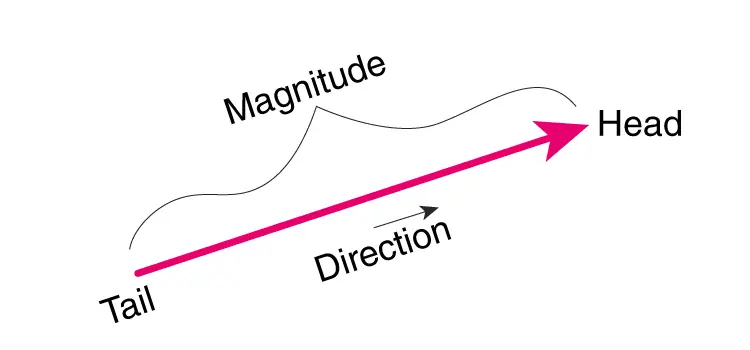
Magnitude of a Vector
We already know that a vector is an object that has both size and direction. To figure out how big a vector is, we need to figure out how long it is. Quantities such as velocity, displacement, force, momentum, etc. are vector quantities. But speed, mass, distance, volume, temperature, etc. are scalar quantities. The only thing a scalar has is its size, while vectors have both size and direction.
The argument of Complex Numbers
In math, the complex plane is a very important tool. It is also called the z-plane, which is made up of two lines that are perpendicular to each other and are called axes. The horizontal line is called the real axis because it shows real numbers. The vertical line, on the other hand, represents imaginary numbers and is called an imaginary axis. The complex plane is used to show how complex numbers can be understood from a geometric point of view. This plane is like the Cartesian plane in that it has real and imaginary parts of a complex number and X and Y axes. Complex numbers are related to two different ideas. They are size and point of view. In this article, we’ll talk in detail about what a complex number is, what its properties are, and how to write a formula for it.
Argument of Complex Numbers Definition
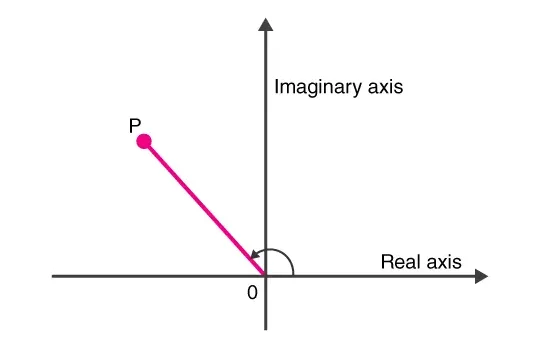
The argument of a complex number is the angle from the real axis in the direction of the complex number as it is shown on the complex plane. It is marked by “” or “”. It is measured using the standard unit called “radians.”
Argument of Complex Numbers Formula
In polar form, a complex number is represented by the equation r(cos θ + i sin θ), here, θ is the argument. The argument function is denoted by arg(z), where z denotes the complex number, i.e. z = x + iy.
The computation of the complex argument can be done by using the following formula:
arg (z) = arg (x+iy) = tan-1(y/x)
Therefore, the argument θ is represented as:
θ = tan-1 (y/x)
Properties of Argument of Complex Numbers
Let us discuss a few properties shared by the arguments of complex numbers. Suppose that z be a nonzero complex number and n be some integer, then
arg(zn) = n arg(z)
Let us assume, z1 and z2 be the two complex numbers, the following identities are:
- arg (z1/ z2) = arg ( z1) – arg ( z2)
- arg ( z1 z2) = arg ( z1) + arg ( z2)
How to Find the Argument of Complex Numbers?
- Find the real and imaginary parts from the given complex number. Denote them as x and y respectively.
- Substitute the values in the formula θ = tan-1 (y/x)
- Find the value of θ if the formula gives any standard value, otherwise write it in the form of tan-1 itself.
- This value followed by the unit “radian” is the required value of complex argument for the given complex number.
Consider the complex number \(z = 3 + 4i\). Let us find the distance of z from the origin:
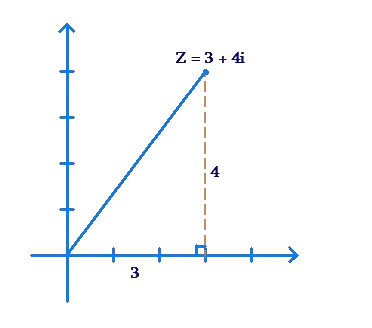
Clearly, using the Pythagoras Theorem, the distance of z from the origin is \(\sqrt {{3^2} + {4^2}} = 5\) units. Also, the angle which the line joining z to the origin makes with the positive Real direction is \({\tan ^{ – 1}}\left( {\frac{4}{3}} \right)\).
Similarly, for an arbitrary complex number \(z = x + yi\), we can define these two parameters:
Modulus of z. This is the distance of z from the origin, and is denoted by \(\left| z \right|\).
Argument of z. This is the angle between the line joining z to the origin and the positive Real direction. It is denoted by \(\arg \left( z \right)\).
Let us discuss another example. Consider the complex number \(z = – 2 + 2\sqrt 3 i\), and determine its magnitude and argument. We note that z lies in the second quadrant, as shown below:
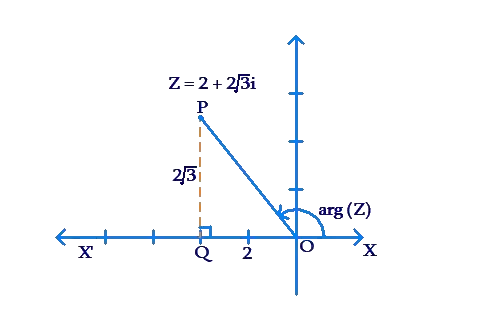
Using the Pythagoras Theorem, the distance of z from the origin, or the magnitude of z, is
\[\left| z \right| = \sqrt {{{\left( { – 2} \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2}} = \sqrt {16} = 4\]
Now, let us calculate the angle between the line segment joining the origin to z (OP) and the positive real direction (ray OX). Note that the angle POX’ is
\[\begin{array}{l}{\tan ^{ – 1}}\left( {\frac{{PQ}}{{OQ}}} \right) = {\tan ^{ – 1}}\left( {\frac{{2\sqrt 3 }}{2}} \right) = {\tan ^{ – 1}}\left( {\sqrt 3 } \right)\\ \qquad\qquad\qquad\qquad\qquad\;\;\,\,\,\,\,\,\,\,\,\, = {60^0}\end{array}\]
Thus, the argument of z (which is the angle POX) is
\[\arg \left( z \right) = {180^0} – {60^0} = {120^0}\]
It is easy to see that for an arbitrary complex number \(z = x + yi\), its modulus will be
\[\left| z \right| = \sqrt {{x^2} + {y^2}} \]
To determine the argument of z, we should plot it and observe its quadrant, and then accordingly calculate the angle which the line joining the origin to z makes with the positive real direction.
Example 1: Determine the modulus and argument of \(z = 1 + 6i\).
Solution: We have:
\[\left| z \right| = \sqrt {{1^2} + {6^2}} = \sqrt {37} \]
Now, the plot below shows that z lies in the first quadrant:
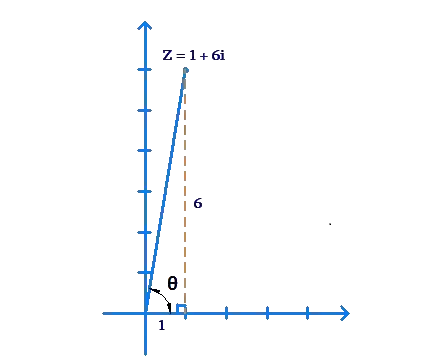
Clearly, the argument of z is given by
\[\arg \left( z \right) = \theta = {\tan ^{ – 1}}\left( {\frac{6}{1}} \right) = {\tan ^{ – 1}}6\]
Example 2: Find the modulus and argument of \(z = 1 – 3i\).
Solution: The modulus is
\[\left| z \right| = \sqrt {{1^2} + {{\left( { – 3} \right)}^2}} = \sqrt {10} \]
Now, we see from the plot below that z lies in the fourth quadrant:
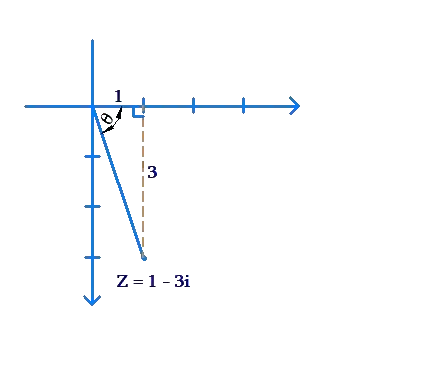
The angle \(\theta \) is given by
\[\theta = {\tan ^{ – 1}}\left( {\frac{3}{1}} \right) = {\tan ^{ – 1}}3\]
Can we say that the argument of z is \(\theta \)? Well, since the direction of z from the Real direction is \(\theta \) measured clockwise (and not anti-clockwise), we should actually specify the argument of z as \( – \theta \):
\[\arg \left( z \right) = – \theta = – {\tan ^{ – 1}}3\]
The significance of the minus sign is in the direction in which the angle needs to be measured. The following example clarifies this further.
Example 3: Find the moduli (plural of modulus) and arguments of \({z_1} = 2 + 2i\) and \({z_2} = 2 – 2i\).
Solution: We have:
\[\begin{align}&\left| {{z_1}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 2 \right)}^2}} = \sqrt 8 = 2\sqrt 2 \\&\left| {{z_2}} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( { – 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2 \end{align}\]
The moduli of the two complex numbers are the same. This is evident from the following figure, which shows that the two complex numbers are mirror images of each other in the horizontal axis, and will thus be equidistant from the origin:
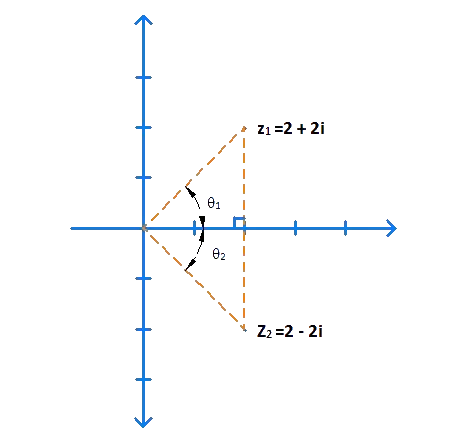
Now, we note that
\[{\theta _1} = {\theta _2} = {\tan ^{ – 1}}\left( {\frac{2}{2}} \right) = {\tan ^{ – 1}}1 = \frac{\pi }{4}\]
Thus,
\[\begin{align}&\arg \left( {{z_1}} \right) = {\theta _1} = \frac{\pi }{4}\\&\arg \left( {{z_2}} \right) = – {\theta _2} = – \frac{\pi }{4}\end{align}\]
We have seen examples of argument calculations for complex numbers lying the in the first, second and fourth quadrants. Let us see how we can calculate the argument of a complex number lying in the third quadrant.

